Arbres

Notions introduites

• Arbres : structures hiérarchiques ;
• Arbres binaires : nœuds, racines, feuilles, sous-arbres gauches, sous-arbres droits ;
• Taille et hauteur d’un arbre ;
• Parcours un arbre de différentes façons (ordres infixe, préfixe ou suffixe ; ordre en largeur d’abord) ;

1) Structure arborescente.

Les structures arborescentes forment une autre famille de structure chaînée que celle des listes, dans lesquelles le nombre de sauts à effectuer pour aller depuis le point de départ jusqu’à une position souhaitée est potentiellement bien moindre que pour une liste. Ces structures sont omniprésentes en informatique : l’arborescence des fichiers par exemple.
Celle-ci permet notamment, partant du répertoire racine et en avançant de répertoire en sous répertoire, d’accéder en un petit nombre d’étapes à n’importe quel fichier choisir parmi des dizaines de milliers.

Arborescence des fichiers sous Linux

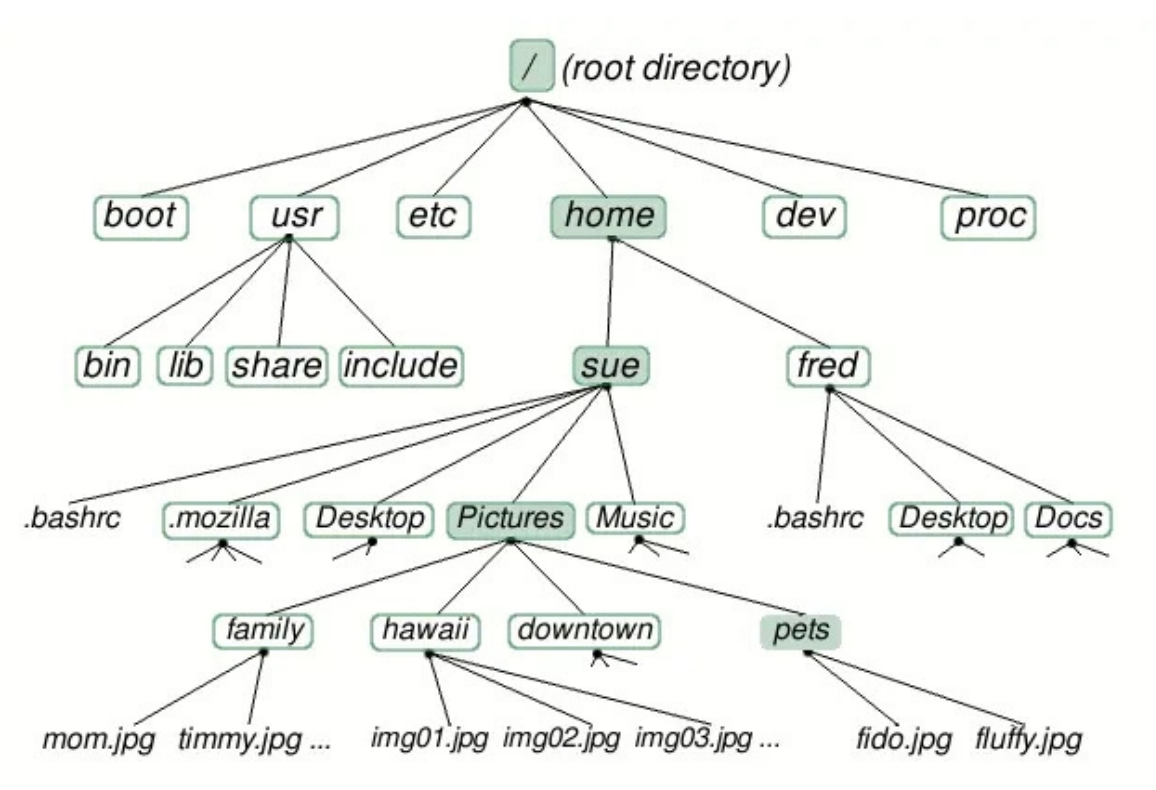
Cette structure de donnée permet également une organisation hiérarchique de l’information, qui la rend utile pour représenter des programmes, le contenu de pages web, des bases de données (fichiers XML, JSON,...)

Définition 1:

Une arborescence ou un arbre est un ensemble non vide de nœuds qui sont organisés de la façon suivante :

• un nœud particulier est la racine de l’arborescence ;
• les autres nœuds sont des sous-ensembles distincts qui forment autant d’arborescences ;
• le nœud racine est relié aux autres racines de ses sous-arborescences qu’on appelle ses fils ;
• un nœud n’ayant pas de fils est appelé une feuille ;
• chaque nœuds sont reliés par des arêtes.
  On a ici une définition récursive.

Définition 2 :

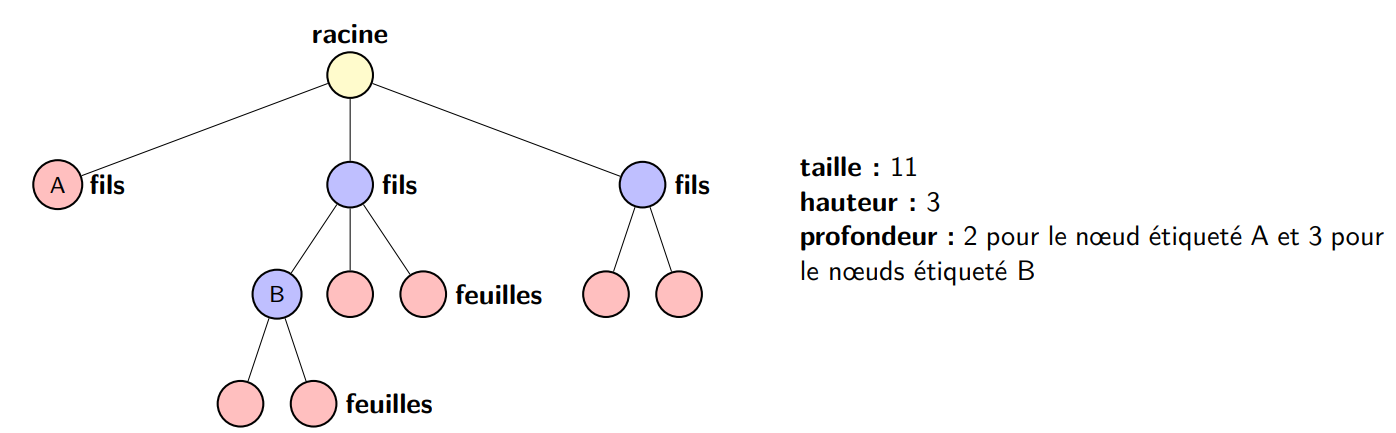
On définit également les notions suivantes :

• la taille d’un arbre est son nombre de nœuds ;
• la hauteur d’un arbre est le plus le nombre maximal d’arêtes qu’on peut suivre d’une feuille jusqu’à la racine ;
• la profondeur d’un nœud est le nombre de nœuds rencontrés en descendant depuis la racine jusqu’à ce nœud.

2) Les Arbres binaires.

Un arbre binaire est un cas particulier d’arborescence dans laquelle chaque nœud possède au plus deux fils. La racine est reliée à deux sous-arbres binaires appelés respectivement sous-arbre gauche et sous-arbre droit.
L’arbre vide ne contient aucun nœud, la racine d’un arbre non vide est l’équivalent de la tête d’une liste non vide.
Voici quelques exemples d’arbres binaires :

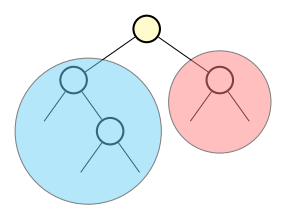
Les sous-arbres d'un arbre	Exemple d'un arbre peigne
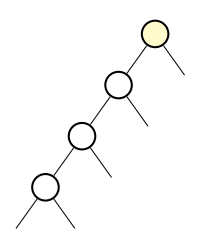Arbre binaire à 4 nœuds avec le sous-arbre gauche de sa racine dans le cercle bleu et le sous-arbre droit dans le cercle rouge.	Arbre binaire où le sous-arbre non vide est systématiquement du même côté (ici à gauche) : un peigne. Sa hauteur \(h\) est égale à sa taille \(N\), sa structure est similaire à celle d’une liste chaînée.

2.1) Arbre binaire parfait.

Dans un arbre binaire parfait toutes les feuilles sont à la même profondeur.
Dans cet exemple, la hauteur de l’arbre est \(h = 3\) et sa taille $N se calcule ainsi :

\(N = 1 + 2 + 2^2 + 2^3 = \overset{3}{\underset{i=0}{\sum}}2^i = \frac{2^4 - 1}{2 - 1} = 2^4 - 1 = 15\)

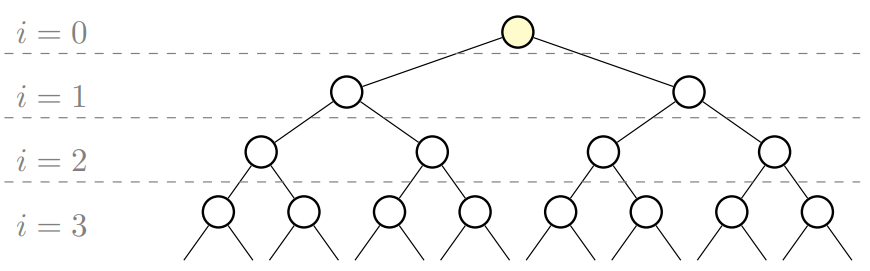
De manière générale, pour un arbre binaire parfait, sa taille \(N\) et sa hauteur \(h\) vérifient \(N = 2^{h+1} − 1\). En effet :

\(N = 1 + 2 + 2^2 + ... + 2^h = \overset{h}{\underset{i=0}{\sum}}2^i = \frac{2^{h+1} - 1}{2 - 1} = 2^{h+1} - 1\)

2.2) Calcul de la taille et de la hauteur d'un arbre.

Pour une hauteur donnée, la taille d'un arbre quelconque est toujours comprise entre la taille d'un arbre peigne (\(h+1\)) et celle de l'arbre parfait (\(2^{h+1}-1\)) :

\(h+1 \geqslant N \geqslant 2^{h+1}-1\)

Voici les deux algorithmes pour les calculs de la taille et de la hauteur d’un arbre binaire, a désigne un arbre de racine racine(a), de fils gauche gauche(a) et de fils droit droite(a) :

3) Parcours d'un arbre binaire.

3.1) Parcours en largeur d'abord.

Ce parcours essaie toujours de visiter le nœud le plus proche de la racine qui n’a pas déjà été visité. En suivant ce parcours, on va d’abord visiter la racine, puis les nœuds à la profondeur 1, puis 2, etc. D’où le nom parcours en largeur.
Dans ce cas, l’ordre de visite des nœuds serait le suivant : A B G C F H I D E E.
L’algorithme de parcours en largeur utilise une File.

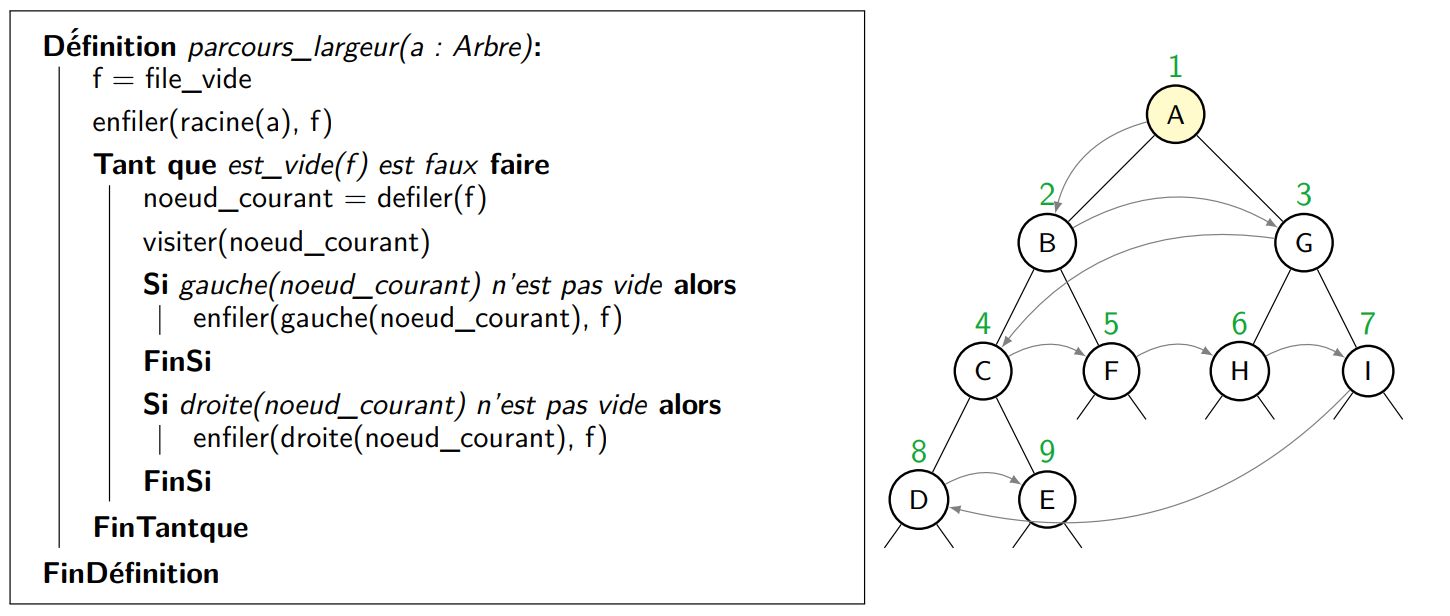
3.2) Parcours en profondeur préfixe.

Ce parcours visite le nœud courant puis ses fils gauche et droit, l’ordre de visite est : A B C D E F G H I.
Les algorithmes de parcours en profondeur sont récursifs, c’est la position de la visite du nœud dans l’algorithme qui change :

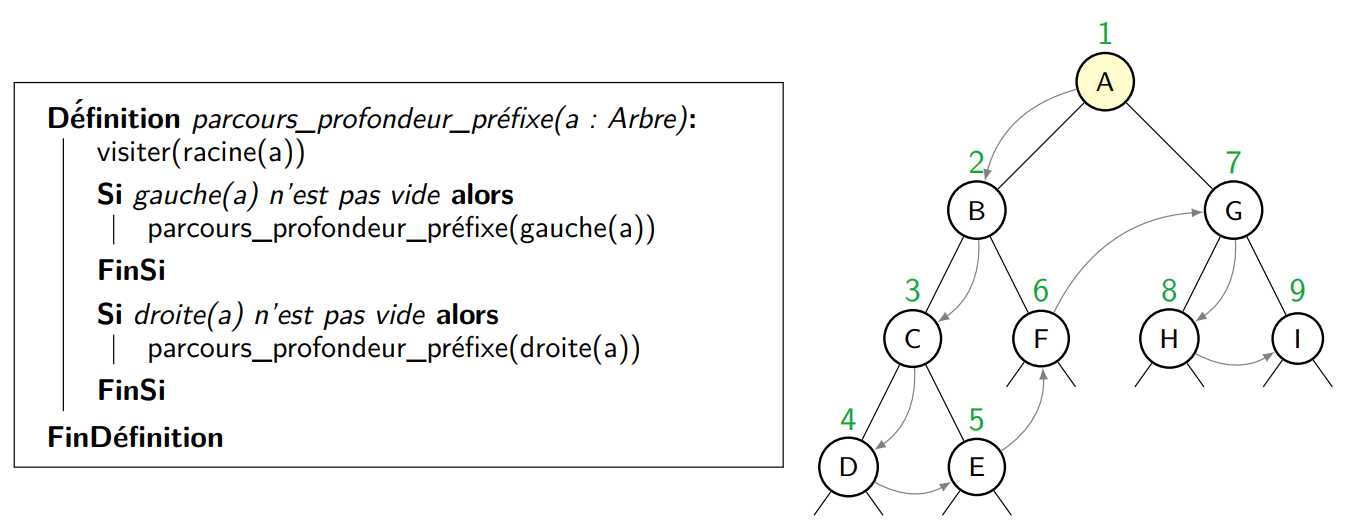
3.3) Parcours en profondeur suffixe ou postfixe.

Ce parcours visite d’abord les fils gauche et droit puis le nœud courant, l’ordre de visite est : D E C F B H I G A.

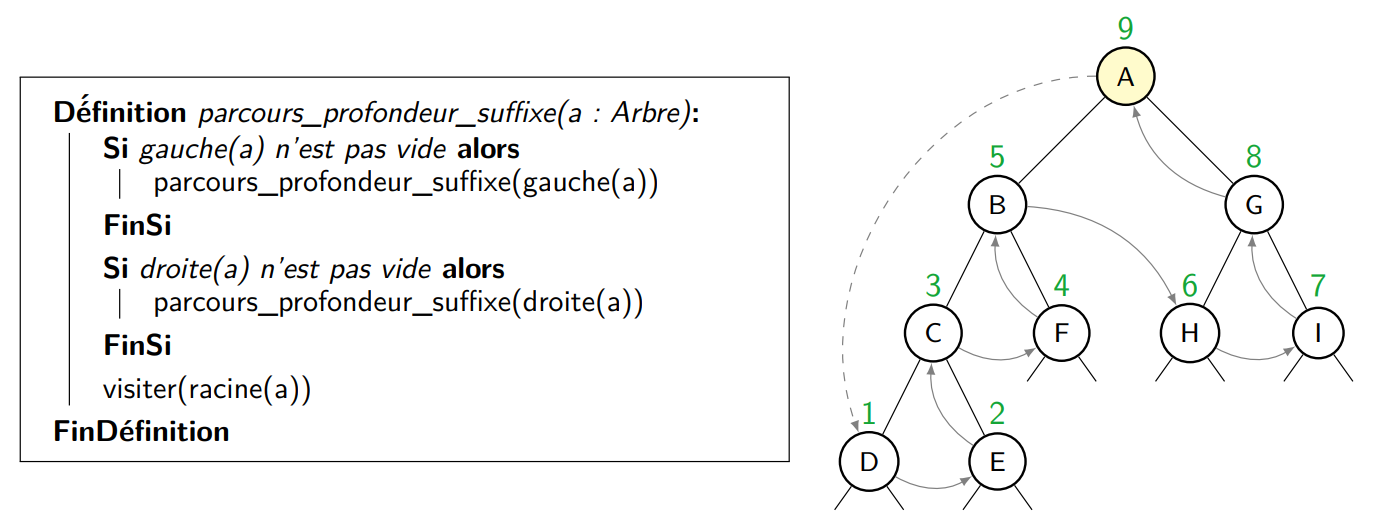
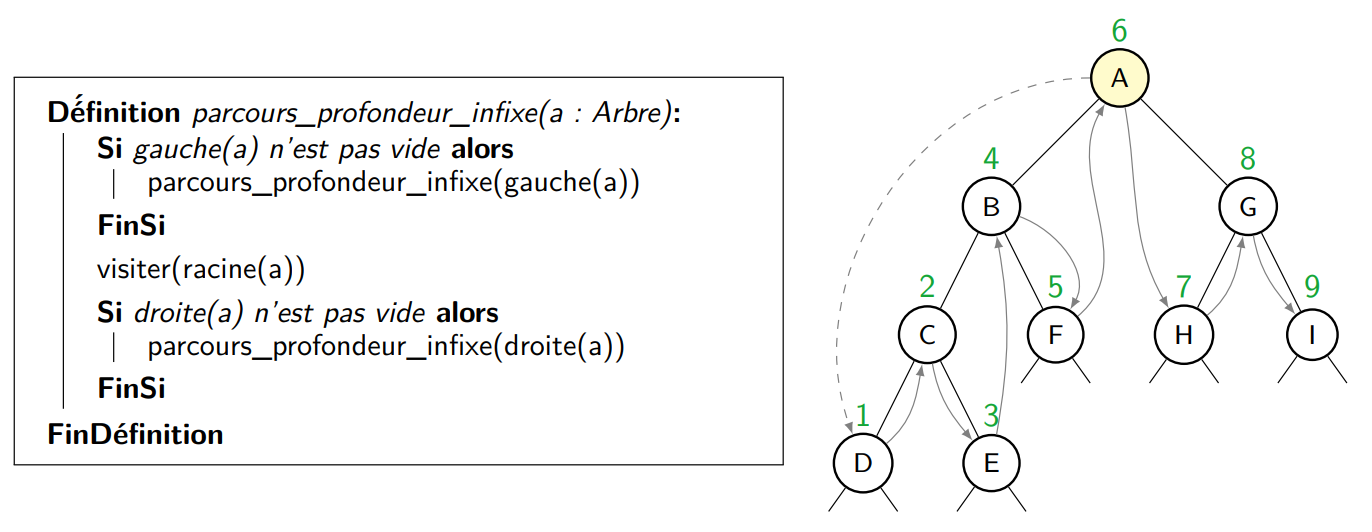
3.4) Parcours en profondeur infixe.

Ce parcours visite d’abord le fils gauche, le nœud courant, puis le droit, l’ordre de visite est : D C E B F A H G I.

3.5) Remarque.

La différence entre les algorithmes des différens parcours en profondeur se trouve dans la position de l'action de visiter le noeud :

• Parcours préfixe : on commence par visiter le noeud,
• Parcours suffixe : on visite le noeud après avoir parcouru l'arbre gauche et l'arbre droit,
• Parcours infixe : on visite le noeud entre le parcours de l'arbre gauche et celui de l'arbre droit.