Aller au contenu

Calculabilité⚓︎

I - Quelques repères historiques de la calculabilité⚓︎

1

  • Wilhelm Schickard (1592 - 1635)}, professeur à l'Université de Tübingen (Allemagne), aurait dessiné les plans de la première machine à calculer (mécanique). Cette machine n'a pas été construite.
  • Blaise Pascal (1623 - 1662), mathématicien et philosophe, construit à l?age de 19 ans la Pascaline, première machine à calculer opérationnelle du XVIIè siècle
  • Gottfried Wilhelm Leibniz (1646 - 1716), mathématicien et philosophe, développe aussi une machine à calculer. Il préconise des idées très modernes : la machine de calcul universelle, le schéma "entrée-calcul-sortie", la base 2 pour la représentation des nombres.
  • Le métier à tisser de Joseph Marie Jacquard (1752 - 1834) est basé sur l'utilisation de cartes perforées, et est à l'origine des premiers programmes de calcul.
  • Charles Babbage (1791 - 1871), professeur à Cambridge, construit la machine différentielle et imagine les plans de la machine analytique (machine programmable). Cette dernière peut être considérée comme précurseur des ordinateurs modernes, consistant d'une unité de contrôle, une unité de calcul, une mémoire, ainsi que l'entrée-sortie.

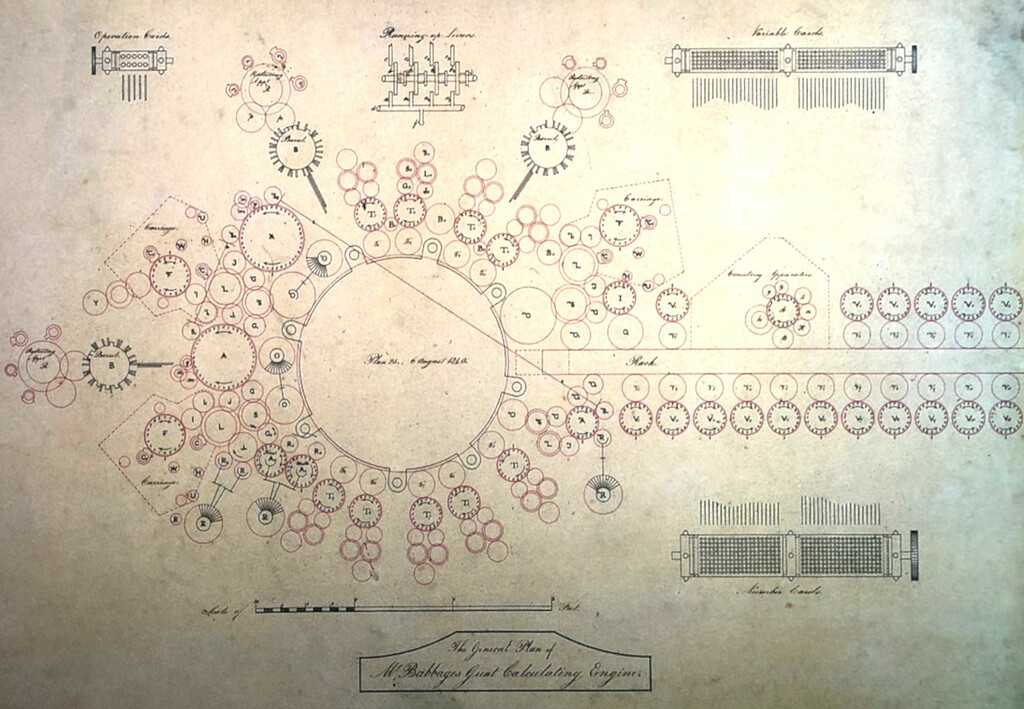
Machine de BabbageCharles Babbage

  • Ada Lovelace (1815 - 1852) , est une pionnière de la science informatique. Elle est principalement connue pour avoir réalisé le premier véritable programme informatique, lors de son travail sur un ancêtre de l'ordinateur : la machine analytique de Charles Babbage. Dans ses notes, on trouve en effet le premier programme publié, destiné à être exécuté par une machine, ce qui fait considérer Ada Lovelace comme le premier programmeur du monde. Elle a également entrevu et décrit certaines possibilités offertes par les calculateurs universels, allant bien au-delà du calcul numérique et de ce qu'imaginaient Babbage et ses contemporains. Elle est assez connue dans les pays anglo-saxons et en Allemagne, notamment dans les milieux féministes ; elle est moins connue en France, mais de nombreux développeurs connaissent le langage Ada, nommé en son honneur.

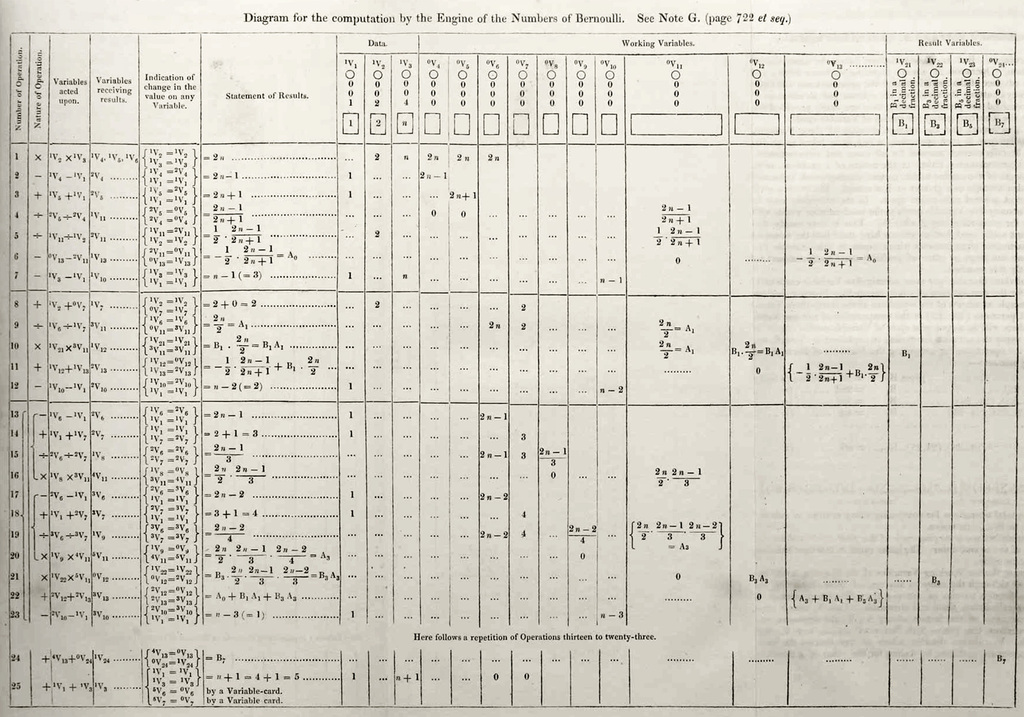
Premier programmeAda Lovelace

  • David Hilbert (1862 - 1943}, mathématicien allemand. En 1900, Hilbert propose 23 problèmes dont certains ne sont pas résolus à ce jour. Il présente en 1920 un programme de recherche visant à clarifier les fondements des mathématiques : "tout énoncé mathématique peut être soit prouvé ou réfuté". Plus tard il énonce le "Entscheidungsproblem" : montrer de façon "mécanique" si un énoncé mathématique est vrai ou faux. Il faudra attendre 1936 pour qu'Alan Turing s'intéresse au problème n\(^{\circ}\)10 avec Church (dont il était le doctorant). Ils définissent rigoureusement la notion d'algorithme.
  • Kurt Gödel (1906 - 1978), un des logiciens les plus fameux de l'histoire, répond 1931 négativement quand au programme proposé par Hilbert, en montrant que tout système formel suffisamment puissant est soit incomplet, soit incohérent. Il montre ceci en construisant une formule qui exprime le fait qu'elle n'est pas démontrable.

Alan Turing

  • Alan Turing (1912 - 1954) et Alonzo Church (1903 - 1995) montrent indépendamment, en 1936, l'indécidabilité de l'Entscheidungsproblem. Turing propose "la machine de Turing" comme modèle mathématique de calcul, et Church le lambda calcul. Ils énoncent le principe selon lequel tout ce qui est calculable peut être calculé sur un de ces deux modèles ("thèse de Church-Turing"). La Machine de Turing est inventée pour répondre au problème mathématiques de la décidabilité proposé par Hilbert. Une machine de Turing a pour but de décrire les algorithmes. Il faut savoir que Turing ne verra pas de son vivant une réalisation concrète de sa "machine".

II - La machine de Turing⚓︎

2

Machine de Turing ENS

© Projet Rubens, ÉNS de Lyon, CC-BY : http://rubens.ens-lyon.fr/

Une vidéo : https://www.youtube.com/watch?v=L5O04P2ASRc

Machine de Turing

Une machine de Turing \(M\) est la donnée de :

  • un ensemble fini d'états \(E_M\) ;
  • un état initial \(I_M \in E_M\) ;
  • un ensemble d'états finaux \(F_M \subset E_M\) ;
  • un alphabet (en général \(\{0;1; \cdot\}\)) ;
  • une fonction de transition : \(\delta_M : (E_M \setminus F_M)\times \{0;1; \cdot\} \rightarrow E_M\times \{0;1; \cdot\}\times \{g;d\}\) avec \(g\) pour gauche et \(d\) pour droite.

La fonction de transition agit sur un ruban qui est une fonction \(r:\mathbb{Z}\ \rightarrow \{0;1;\cdot\}\) à support fini c'est-à-dire \(r(i)=\cdot\) pour presque tout \(i\in\mathbb{Z}\).

Remarque :
On pourrait travailler avec un ensemble de symboles quelconques, les chiffres décimaux : 0, 1, ..., 9 ; tous les caractères disponibles sur un clavier, un seul symbole (trou sur une carte). Cela, ne change rien, nous pouvons tout coder en binaire...

Exemple 1

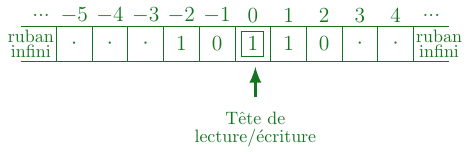
Exemple 1

Table de transition

Pour définir cette fonction de transition et donc la machine de Turing, on peut utiliser une table des transitions.

Elle permet de définir, pour chaque état, selon le résultat de la lecture, les actions à exécuter : écriture, déplacement, choix d'un nouvel état.

Exemple 2

État Lit Écrit Déplace Suivant
\(e_0\) \(1\) \(0\) g \(e_0\)

Ici, \(\delta_M(e_0,1)=(e_0,0,g)\). Ainsi si l'on applique cet état au ruban de l'exemple précédent, nous nous trouverons dans la situation suivante :

Exemple 2

L'automate correspondant à cette table de transitions est représenté ainsi : 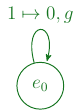Exemple 2 - Automate

Voici encore quelques définitions pour décrire le "calcul" d'une machine de Turing :

Effectuer un calcul à l'aide d'un machine de Turing

  • Une configuration de la machine \(M\) est un couple \((e, r)\) formé d'un état \(e\) et d'un ruban \(r\).
  • La configuration \((e, r)\) est initiale si \(e = I_M\) et finale si \(e \in F_M\) ;
  • Si \((e, r)\) n'est pas finale, on passe à la configuration suivante \((e', r')\) :
    • on calcule la transition : \((e',v',m')=\delta_M(e,r(0))\) ;
    • on met à jour : \(r(0)=v'\) ;
    • on décale :
      • \(r'(i)=r(i+1)\) pour tout \(i\in\mathbb{Z}\) si \(m=g\) ;
      • \(r'(i)=r(i-1)\) pour tout \(i\in\mathbb{Z}\) si \(m=d\) ;

Exercice 1

  1. Écrire la table de transition associée à l'automate ci-dessous.

Exercice 1 - Question 1

    1. Déterminer le résultat que fourni cette machine de Turing pour le ruban ci-dessous :
      Exercice 1 - Question 2

    2. Même question avec ce ruban :
      Exercice 1 - Question 3

    3. Même question avec ce ruban :
      Exercice 1 - Question 4

  2. Que calcule cette machine de Turing ?

Remarque :
On peut décrire une machine de Turing sur un ruban à l'aide uniquement des symboles : , 0 1 . g d
On utilisera le codage : état courant, symbole lu, état suivant, symbole écrit, déplacement. Ainsi, on peut assimiler une machine de Turing à un programme !!!

Exemple 3

Exemple 3

Codage : 0,.,1,1,d,0,0,1,1,d,0,1,0,0,g,1,.,10,.,g,1,0,1,0,d,1,1,1,1,d,

Théorème

Il existe une machine de Turing universelle \(U\) qui à tout couple \((M, r)\mapsto \text{résultat d'exécution de la machine }M\)
où \(M\) est une machine de Turing et \(r\) un ruban.

On dit que la machine \(U\) simule la machine \(M\) en suivant sa description.

Remarque :
Autrement dit \(U\) exécute le programme \(M\) : la machine \(M\) est un programme pour \(U\). Ainsi, un ordinateur, c'est une machine qu'on peut programmer donc un ordinateur est une machine de Turing universelle et écrire un programme ou un algorithme est équivalent à définir une machine de Turing.

Il existe d'autres modèles de calcul :

  • les fonctions récursives (Kurt Gödel)
  • le \(\lambda\)-calcul (Alonzo Church)
  • machines RAM (modèle de nos ordinateurs, Von Neumann)
  • machines à compteurs (Marvin Minsky)
  • les automates cellulaires (ex. : jeu de la vie de Conway)
  • la redstone dans Minecraft
  • tous les langages de programmation
  • ...

Ces modèles décrivent la même notion de calcul !

En résumé

Dans chacun de ces modèles, il y a un programme universel, et un programme universel peut en simuler un autre... Ainsi :

Écrire un programme ou un algorithme est équivalent à définir une machine de Turing.

III - Calculabilité et problème de l'arrêt⚓︎

Thèse de Church-Turing

Les machines de Turing (ou les modèles équivalents) formalisent la notion de méthode effective de calcul ou de calculabilité.

On considère que la \textit{notion intuitive de méthode effective de calcul} correspond aux caractéristiques suivantes : - l'algorithme consiste en un ensemble fini d'instructions simples et précises qui sont décrites avec un nombre limité de symboles ; - l'algorithme doit toujours produire le résultat en un nombre fini d'étapes ; - l'algorithme peut en principe être suivi par un humain avec seulement du papier et un crayon ; - l'exécution de l'algorithme ne requiert pas d'intelligence de l'humain sauf celle qui est nécessaire pour comprendre et exécuter les instructions.

Question : Y a-t-il des fonctions incalculables ? ou des problèmes indécidables ?

Problème de l'arrêt

Le problème de l'arrêt pour un modèle de calcul est une fonction \(A\) qui à tout couple \((P, E)\) où \(P\) est un programme (ou un algorithme ou une machine de Turing) et \(E\) une entrée, renvoie \(1\) si le programme \(P\) termine sur l'entrée \(E\) et \(0\) sinon.

\[A:(P,E) \mapsto\begin{cases}1\text{ si }P(E) \text{ termine}\\0\text{ sinon}\end{cases}\]

Exercice 2

On considère le programme Python suivant :

def P(n):
    s = 0
    i = 0
    while (i < n):
        s = i + s
    return s
Que vaut \(A(P, 0)\) ? Que vaut \(A(P, 1)\) ?

Théorème

Le problème de l'arrêt n'est pas calculable (autrement dit, il n'existe pas de tel foncion \(A\)) ou encore le problème de l'arrêt est indécidable.

Démonstration

Nous allons faire un raisonnement par l'absurde : supposons qu'il existe un tel programme \(A\) pour le calculer et définissons le programme suivant : 

def P(f):
    if A(f,f):
        while True:
            pass
    else:
        return 0

Voyons ce que calcule P(P). Cette fonction est construite de telle manière que si le problème de l'arrêt renvoie 1 (donc True) pour le programme P sur l'entrée P alors la fonction P entre dans une boucle infinie et ne termine pas ce qui est contradictoire, mais dans le cas contraire le programme termine ce qui est également contradictoire.

Dans tous les cas, l'existence d'un programme pouvant calculer le problème de l'arrêt nous conduit à une absurdité, c'est donc que le problème de l'arrêt n'est pas calculable.

Compléments :

Ce cours en PDF

  1. D'après http://www.monlyceenumerique.fr/nsi_terminale/lp/lp1_calculabilite_decidabilite.php ↩

  2. Cette partie et la suivante est largement inspirée du cours de Lionel VAUX lors du DIU EIL organisé par l'université d'Aix-Marseille. ↩