Aller au contenu

La récursivité⚓︎

I - Introduction⚓︎

L'idée sous-jacente de la récursivité est que pour résoudre un problème ou effectuer un calcul, on se ramène à la résolution d’un problème similaire mais de complexité moindre. On recommence ainsi jusqu’à obtenir un problème élémentaire que l'on sait résoudre.

Exemple : La somme des éléments d'une liste

Étant donné une liste d'entiers L = [2, 12, 1, 8], calculer la somme des éléments de cette liste.

Comme les listes sont itérables, nous pouvons simplement résoudre ce problème avec l'un de ces algorithmes que l'on dit itératif :

Exemple 1

ou encore

Exemple 2

Supposons maintenant que nous n'ayons pas la possibilité de faire de "boucles".

On peut alors aborder le problème sous un autre angle :

la somme des termes de cette liste est: 2 + ( la somme des termes de [12, 1, 8])

Soit 2 + (12 + (la somme des termes de [1, 8]) et enfin 2 + (12 + (1 + (la somme des termes de [8])))

Il est clair que : la somme des termes de [8] est 8. Au final le calcul à faire est : 2 + (12 + (1 + (8))) = 23

Considérons alors une fonction somme() et qui renvoie le résultat de la somme des éléments de la liste.

L'algorithme ci-dessous que l'on dit récursif réalise cette seconde approche :

Exemple 3

Exercice 1

  1. Écrire cette fonction somme() en Python, et la tester sur plusieurs exemples.
    En Python l'instruction liste[1:] renvoie la liste sans le premier élément (de l'indice 1 à la fin).

  2. Écrire une nouvelle fonction sommeCarres() calculant la somme des carrés des éléments d'une liste

Fonctions à compléter

### Définition de la fonction Somme()
def 

### Définition de la fonction SommeCarres()


### Quelques exemples pour tester les fonctions
assert somme([2, 12, 1, 8]) == ...
assert sommeCarres([2]) == ...
assert sommeCarres([2, 12, 1, 8]) == 213

II - Fonctionnement des appels récursifs⚓︎

La fonction va s'appeler elle-même avec un paramètre plus "petit". Cet appel en induira un autre, puis un autre, etc. D'appel en appel, la taille du paramètre va ainsi diminuer. On s'arrêtera quand cette taille sera celle d'un problème immédiatement résolvable.

Les différents problèmes intermédiaires, ceux permettant de passer du problème initial au problème élémentaire, sont stockés successivement en mémoire dans ce que l'on appelle une pile. Il s'agit d'une structure de données dans laquelle on accède aux éléments dans l'ordre inverse de leur ajout en mémoire. Dans notre cas, on utilisera ainsi en premier le résultat du problème élémentaire, puis de proche en proche on arrivera à celui du problème initial.

Exemple :

Exécution de la fonction de l'exemple précédent pour liste = [2, 12, 1, 8]

Exemple 4

Comme expliqué précédemment, les différents appels récursifs sont empilés en mémoire jusqu'à ce que le paramètre d’appel est une longueur de 1 (condition d’arrêt). Ils sont ensuite dépilés jusqu’à l'appel initial.

Exercice 2 - Implémentation récursive de la fonction factorielle

Rappelons tout d'abord que \(n!=1\times2\times3\times...\times n\). On montre alors facilement la relation de récurrence \(n!=n\times(n-1)!\)

Si l'on sait calculer \((n-1)!\) on connaîtra donc la valeur de \(n!\)

Or, toujours d'après la formule de récurrence, \((n-1)!=(n-1)\times(n-2)!\)

On est donc ramené au calcul de \((n-2)!\) Et ainsi de suite jusqu'à \(1!\) dont on connaît la valeur : \(1\).

  1. Écrire l'implémentation Python de cette fonction :
    ### Définition de la fonction
def factoriel(n : int):
    """
    Par définition n!=n*(n-1)! et 1!=1
    """
### Quelques tests
assert factoriel(1) == 1
assert factoriel(5) == 120
  2. Écrire sur une feuille la pile des appels récursifs de cette fonction pour n = 4.

Attention !!!

Il est indispensable de prévoir une condition d’arrêt à la récursion sinon le sous-programme va s'appeler une infinité de fois.

Exemple : Une erreur à ne pas commettre

On a omis ici la condition d'arrêt, cette fonction ne se terminera en théorie donc jamais :

def factorielBad(n):
    return n*factorielBad(n-1)

En pratique, la pile où sont stockés les appels récursifs étant de taille finie, une fois qu'elle sera pleine le programme ne répondra plus.

II - Récursivité versus itération⚓︎

Par opposition, on qualifiera d'itératif un sous-programme qui ne s'appelle pas

On peut démontrer qu'il est toujours possible de transformer un algorithme récursif en un algorithme itératif et inversement.

L'algorithme itératif sera plus rapide une fois implémenté dans un langage de programmation mais souvent plus complexe à écrire.

Exemple : Implémentation itérative de la fonction factorielle

Cette fois ci on utilise une structure itérative pour effectuer le calcul :

def factorielleIterative(n):
    resultat = 1
    for i in range(2, n+1):
        resultat = resultat*i
    return resultat

Il est manifeste que cette version est beaucoup moins élégante que la précédente.

Évoquons à présent quelques arguments en faveur puis en défaveur de l'usage de la récursivité.

Comme nous l'avons déjà mentionné, cette technique de programmation est très élégante et lisible. Elle évite en effet souvent le recours à de nombreuses structures itératives. Elle est d'autre part très utile voire indispensable pour concevoir des algorithmes sur des structures de données complexes comme les listes, les arbres et les graphes.

Nous reviendrons sur ces différentes structures de données dans les cours sur les graphes et d'algorithmique avancée.

L'inconvénient majeur de la récursivité est qu'une fois cette technique implémentée dans un langage de programmation, elle est très "gourmande" en mémoire. Rappelons en effet que l’on doit empiler tous les appels récursifs. Des débordements de capacité peuvent donc se produire s'il arrive que cette pile soit pleine.

On apprendra à implémenter de façon plus satisfaisante des sous-programmes récursifs afin entre autres d'être beaucoup moins dépendant de la dimension de cette pile. Il s'agit d'une technique appelée programmation dynamique.

Exercice 3 - Déterminer le minimum d'une liste d'entiers

Supposons que nous ayons une fonction min(a,b) qui renvoie le plus petit des entiers a et b et une liste \(L = [a_0, a_1, ...,a_{n-1} ]\) d'entiers dont il faut déterminer le minimum.

  • Version itérative

    On initialise le minimum à \(\text{mini} = a_0\) On parcours la liste en appelant à chaque étape : \(min(mini, a_i)\)

  • Version récursive

    Le minimum de la liste \(L\) est le minimum entre \(a_0\) et le minimum de la liste \(L'=[a_1, a_2, ..., a_{n-1}]\) qui est lui même le minimum entre et le minimum de la liste et ainsi de suite... La condition d'arrêt étant : s'il n'y a qu'un seul élément dans la liste alors le minimum de la liste est cet élément.

  1. Écrire ces deux fonctions : 

### Définition de la fonction minit - Version itérative
def miniit(L : list) -> int:
    
    
### Définition de la fonction minrec - Version récursive    
def minirec(L : list) -> int:
    
    
### Quelques tests
assert miniit([2, 1, 3, 5]) == 1
assert minirec([2, 1, 3, 5]) == 1

from random import randint
L = [randint(1,100) for i in range(100)]
print(L)
print(miniit(L))
print(minirec(L))
2. Écrire sur une feuille la pile des appels récursifs la fonction minirec, pour la liste [2, 1, 3, 5], sur le modèle de l'exemple donné pour la fonction somme.

Exercice 4 - La suite de Fibonacci

La suite de Fibonacci est la suite \((u_n)\) définie sur \(\mathbb{N}\) de la manière suivante : \(\(\begin{cases} u_0=0\ \text{et}\ u_1=1 \\ u_{n}=u_{n-1}+u_{n-2}\ \text{si}\ n\geqslant2 \end{cases}\)\)

Ses premiers termes sont 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

  1. Écrire l'implémentation récursive d'une fonction donnant le terme de rang \(n\) de la suite de Fibonacci : 
    ### Définition de la fonction
def fibo_rec(n : int) ->int:
    """    Implémentation récursive de la suite de Fibonacci    
    """

    
### Quelques tests :
assert fibo_rec(0) == 0
assert fibo_rec(1) == 1
assert fibo_rec(9) == 34
    Si l'on veut savoir quels sont les appels récursifs effectués lors de l’appel de cette fonction pour n=7, nous pouvons représenter ces appels sous forme d'un arbre, où chaque sommet correspondra à un appel et contiendra la valeur du paramètre à cet instant.

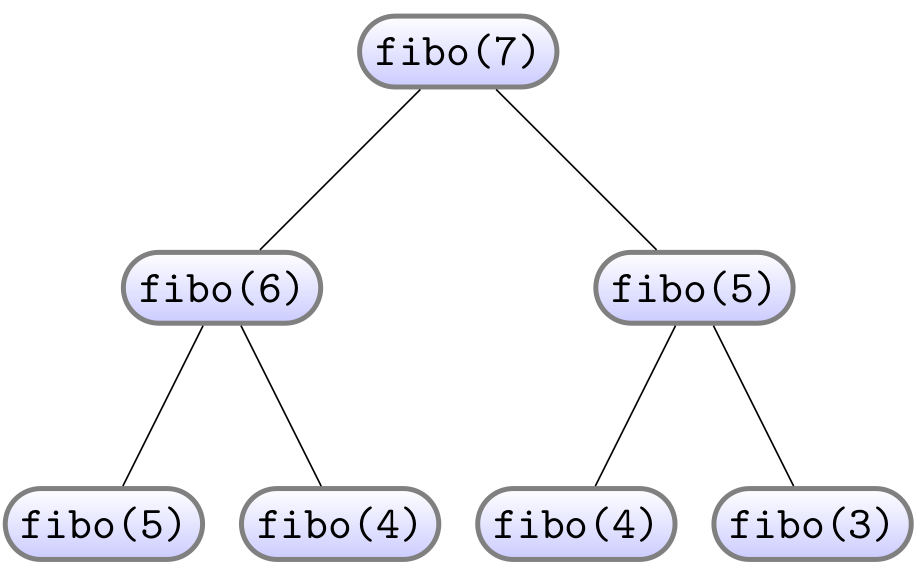
Exercice 4

  1. Le début de cet arbre est donné ci-dessus, le recopier puis le compléter pour obtenir tous les appels récursifs de cette fonction lorsque n=7.
  2. Écrire l'implémentation itérative d'une fonction donnant le terme de rang n de la suite de Fibonacci, puis observer la différence de comportement de ces deux fonctions lors de l'appel pour n=30. 
    ### Définition de la fonction
def fibo_it(n : int) ->int:
    """    Implémentation itérative de la suite de Fibonacci    
    """
    # à compléter
### Quelques tests :
assert fibo_it(0) == 0
assert fibo_it(1) == 1
assert fibo_it(9) == 34

Remarque : Vous constaterez que le temps de calcul par la méthode récursive est extrêmement long, nous verrons comment éviter de faire autant de calcul inutiles car déjà réalisée lorsque nous étudierons la programmation dynamique.

III - Les tours de Hanoï⚓︎

Commencez par regarder la vidéo suivante :

alt

Exercice 5 : Analyse d'un algorithme récursif

Voici l'implémentation en Python de cet algorithme récursif pour résoudre le problème des tours de Hanoï.

  1. Exécuter le programme suivant et observer le résultat : 
    def hanoi(n, X, Y, Z):
    """
    Cette fonction affiche les déplacements à effectuer
    pour résoudre le problème des tours de Anoï comportant
    n cylindres, les variables X, Y et Z représentent le
    nom (chaine de caractères str)
    que l'on donne à chacun des piquets. X étant le
    piquet de départ, Y celui d'arrivé et Z le piquet intermédiaire
    """
    if n == 1:
        print(f"Déplacer le disque 1 de {X} à {Y}")
    else:
        hanoi(n-1, X, Z, Y)
        print(f"Déplacer le disque {n} de {X} à {Y}")
        hanoi(n-1, Z, Y, X)

hanoi(4,'D','A','I')
    Sortie : 
    Déplacer le disque 1 de D à I
Déplacer le disque 2 de D à A
Déplacer le disque 1 de I à A
Déplacer le disque 3 de D à I
Déplacer le disque 1 de A à D
Déplacer le disque 2 de A à I
Déplacer le disque 1 de D à I
Déplacer le disque 4 de D à A
Déplacer le disque 1 de I à A
Déplacer le disque 2 de I à D
Déplacer le disque 1 de A à D
Déplacer le disque 3 de I à A
Déplacer le disque 1 de D à I
Déplacer le disque 2 de D à A
Déplacer le disque 1 de I à A
  2. Voici l'arbre, incomplet, décrivant l'exécution de cette fonction pour les paramètres (4, 'D', 'A', 'I').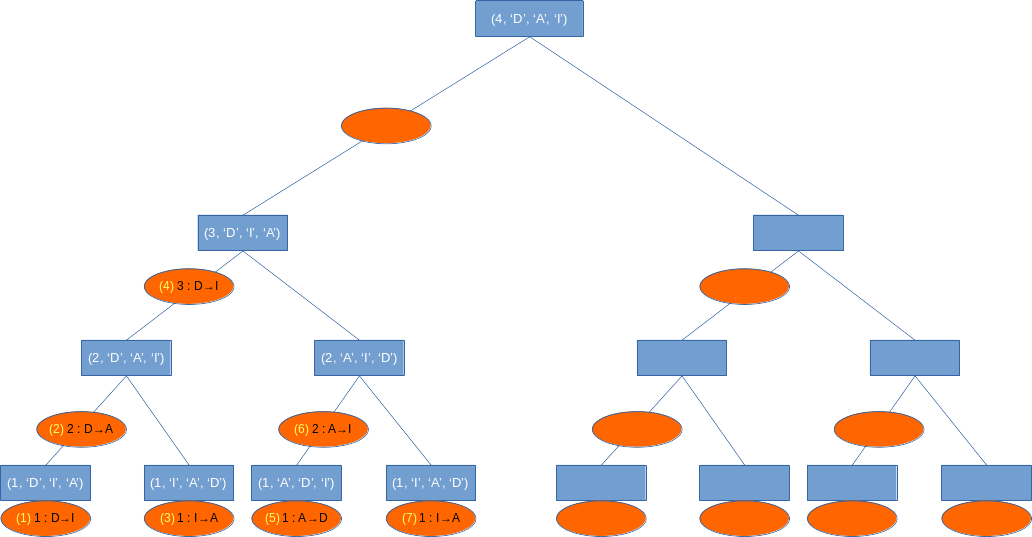 Exercice 5

Les rectangles bleus contiennent les différentes valeurs des paramètres lors des appels récursifs, et les ellipses contiennent l'affichage dans la console ainsi que l'ordre d'affichage.
Compléter cet arbre (un pdf à imprimer est disponible)

Exercice 6 - Flocon de Von-Koch

Faire le TP sur le flocon de Von-Koch avec l'éditeur Spyder.

Cours

Exercices PDF

TP : Le flocon de Von-Koch